Análisis rápido de loterías
¡Hola a todos! Hoy me he lanzado a la piscina de las palabras para traeros un artículo que nació mientras veía las noticias sobre el sorteo de la Lotería de Navidad. ¿Quién no ha soñado alguna vez con que le toque la lotería? Pero, ¿alguna vez te has parado a pensar en las verdaderas probabilidades de que eso ocurra?
En este artículo, vamos a sumergirnos en el fascinante mundo de los sorteos de lotería. He recopilado información sobre los sorteos más populares, incluyendo su precio y el premio medio. Sí, ya sé que los premios varían, pero para no volvernos locos con los cálculos, vamos a trabajar con promedios.
Ahora, prepárate para un viaje visual donde los números cobrarán vida. ¿Sabías que las probabilidades de ganar en algunos de estos sorteos son tan bajas que podrías tener más posibilidades de ser alcanzado por un rayo? Pero tranquilo, no es mi intención desanimarte, sino todo lo contrario. Quiero que veas estos números como un desafío divertido y, quién sabe, quizás descubras que tienes más suerte de lo que pensabas.
A través de gráficos coloridos, comparaciones curiosas y alguna que otra broma (porque, seamos sinceros, a veces reírse de las probabilidades es lo único que nos queda), te llevaré de la mano por este camino de números y sueños.
Al final del artículo, espero que no solo te hayas entretenido, sino que también hayas aprendido algo nuevo. Y recuerda, aunque las probabilidades no siempre estén a nuestro favor, la esperanza y el buen humor nunca deben perderse.
Así que, sin más preámbulos, ¡vamos allá!
Lo primero son los datos que usaremos, que son estos :
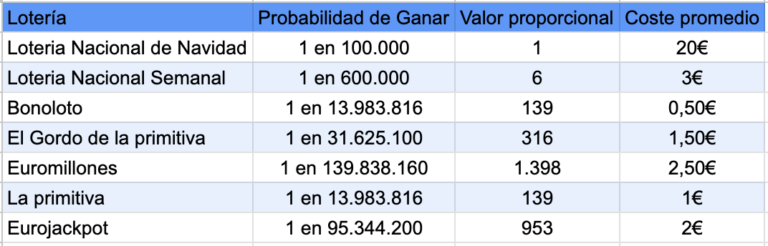
Para analizar las loterías, dividiremos nuestro estudio en dos bloques principales:
- Probabilidad de Ganar: Este bloque se enfoca en las probabilidades matemáticas de ganar en cada tipo de lotería. Aquí, examinaremos las cifras como “1 en 100,000” o “1 en 139,838,160” para entender cuán probable (o improbable) es acertar el premio mayor en cada sorteo. Este análisis nos dará una perspectiva clara sobre las expectativas reales de ganar en cada juego.
- Relación entre Inversión y Ganancia Potencial: En este segundo bloque, analizaremos la relación entre lo que se invierte al comprar un boleto y lo que potencialmente se podría ganar. Este análisis incluirá el costo promedio de una apuesta en cada lotería y comparará este gasto con el premio promedio que se podría obtener. Este enfoque nos ayudará a entender no solo la magnitud de las ganancias posibles, sino también a evaluar si la inversión en un boleto de lotería puede considerarse razonable o desproporcionada en relación con el premio que se ofrece.
Al abordar estos dos bloques, podremos tener una visión integral y equilibrada sobre las loterías, comprendiendo tanto las probabilidades de éxito como la relación costo-beneficio de participar en ellas.
PROBABILIDAD DE GANAR
Para ilustrar efectivamente las diferencias en las probabilidades de ganar en distintas loterías, utilizaremos dos enfoques visuales:
- Comparación Directa: En la primera imagen, mostraremos una comparación directa de las probabilidades de ganar en cada lotería. Esta representación gráfica permitirá ver de manera inmediata cuál es la lotería con la mayor probabilidad de ganar y cuál tiene la menor. Por ejemplo, se puede representar cada lotería con barras de diferente longitud, donde una barra más larga indica una mayor probabilidad de ganar. Esta imagen proporcionará una visión clara y sencilla de las diferencias entre las loterías.
- Escala Logarítmica: Dado que las diferencias en las probabilidades pueden ser enormes (por ejemplo, comparar una probabilidad de 1 en 100,000 con una de 1 en 139,838,160), una escala lineal puede no ser suficiente para apreciar las diferencias más sutiles entre algunas loterías. Por ello, en la segunda imagen, utilizaremos una escala logarítmica. Esta escala es especialmente útil para representar datos con un amplio rango de valores, ya que reduce la disparidad visual entre números muy grandes y pequeños. Con esta representación, los lectores podrán comprender mejor cómo se relacionan las probabilidades entre sí, incluso cuando las diferencias son extremadamente grandes.
Estas dos representaciones visuales complementarias ofrecerán a los lectores una comprensión más profunda y matizada de las probabilidades en los juegos de lotería, desde una perspectiva tanto absoluta como relativa.
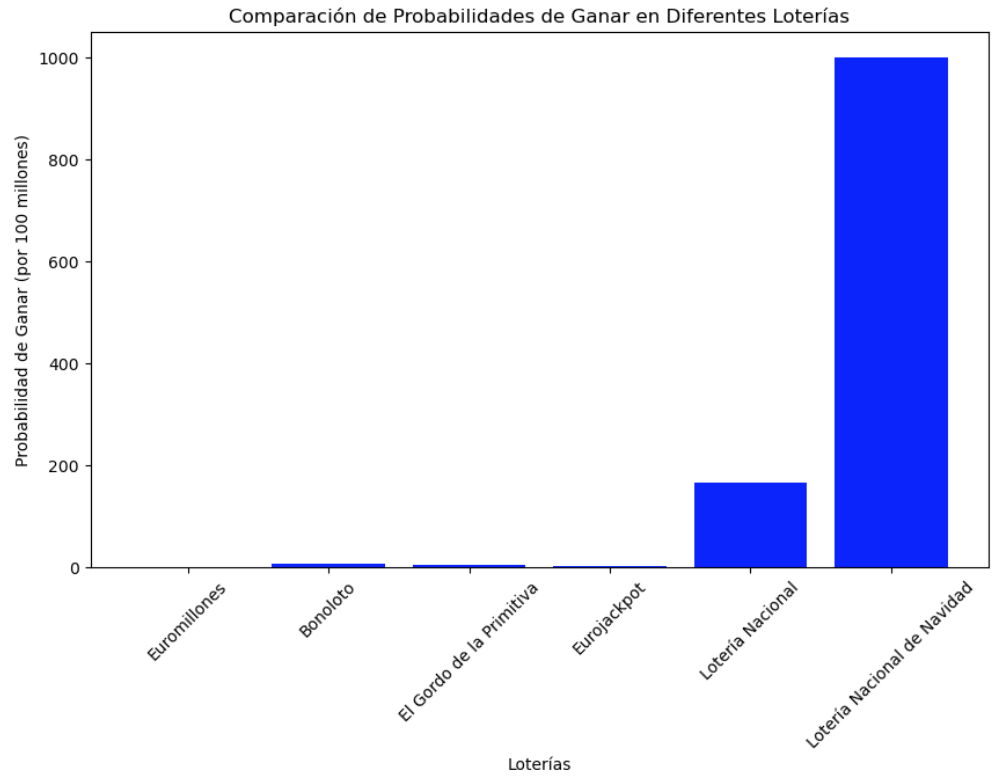
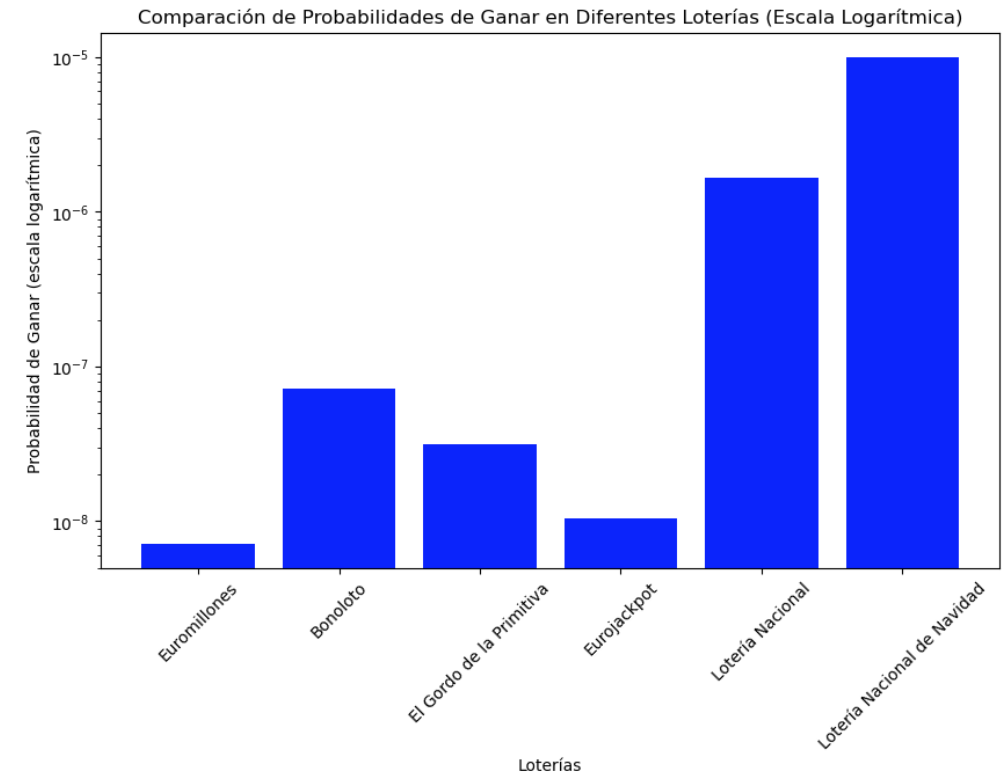
Como podemos observar en el análisis, la Lotería Nacional, y en particular la Lotería Nacional de Navidad, presenta una probabilidad significativamente más alta de ganar en comparación con otras loterías, especialmente cuando la contrastamos con la de Euromillones. Este dato es crucial y sirve como puente hacia el otro bloque de nuestro análisis.
En el siguiente bloque, exploraremos cómo esta mayor probabilidad de ganar en la Lotería Nacional y la Lotería de Navidad se relaciona con la inversión realizada y el retorno potencial. Es decir, aunque estas loterías ofrezcan mayores probabilidades de ganar, es importante considerar qué tan grande es el premio en relación con el costo del boleto y cómo esto se compara con loterías como Euromillones, donde las probabilidades de ganar son menores, pero los premios potenciales son mucho mayores.
Este enfoque nos permitirá entender no solo las probabilidades en sí, sino también el valor relativo de cada apuesta en términos de su potencial retorno económico. Este análisis integral es esencial para cualquier persona interesada en participar en juegos de lotería, proporcionando una visión completa que va más allá de la simple probabilidad de ganar.
RATIO DE GANANCIA
Ahora, abordaremos la relación del ratio de ganancia en las loterías, una métrica que considera tanto la inversión inicial (el coste del boleto) como el premio potencial a ganar. Para esto, utilizaremos la fórmula simple:
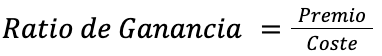
Esta fórmula nos ayuda a entender cuánto podríamos ganar por cada euro invertido en un boleto de lotería. Por ejemplo, si el premio es de 100€ y el boleto cuesta 10€, el ratio de ganancia sería 10. Esto significa que, en teoría, por cada euro gastado, podrías ganar 10 euros.
Es importante destacar que este ratio es una forma de medir la “eficiencia” de una apuesta en términos de su retorno potencial. Un ratio más alto indica un mayor retorno potencial por cada euro invertido, mientras que un ratio más bajo sugiere un retorno menor.
Para visualizar cómo se comparan las diferentes loterías bajo este criterio, presentaremos un diagrama de barras. En este gráfico, cada lotería tendrá una barra cuya longitud representa su ratio de ganancia. Esto permitirá a los lectores comparar de manera rápida y visual cuáles loterías ofrecen un mejor retorno potencial en relación con el coste de sus apuestas.
Este análisis es fundamental para comprender no solo las probabilidades de ganar, sino también el valor potencial de los premios en relación con la inversión realizada. Al combinar este enfoque con el análisis de probabilidades, los lectores podrán tener una visión más completa y equilibrada sobre qué esperar al participar en diferentes juegos de lotería.
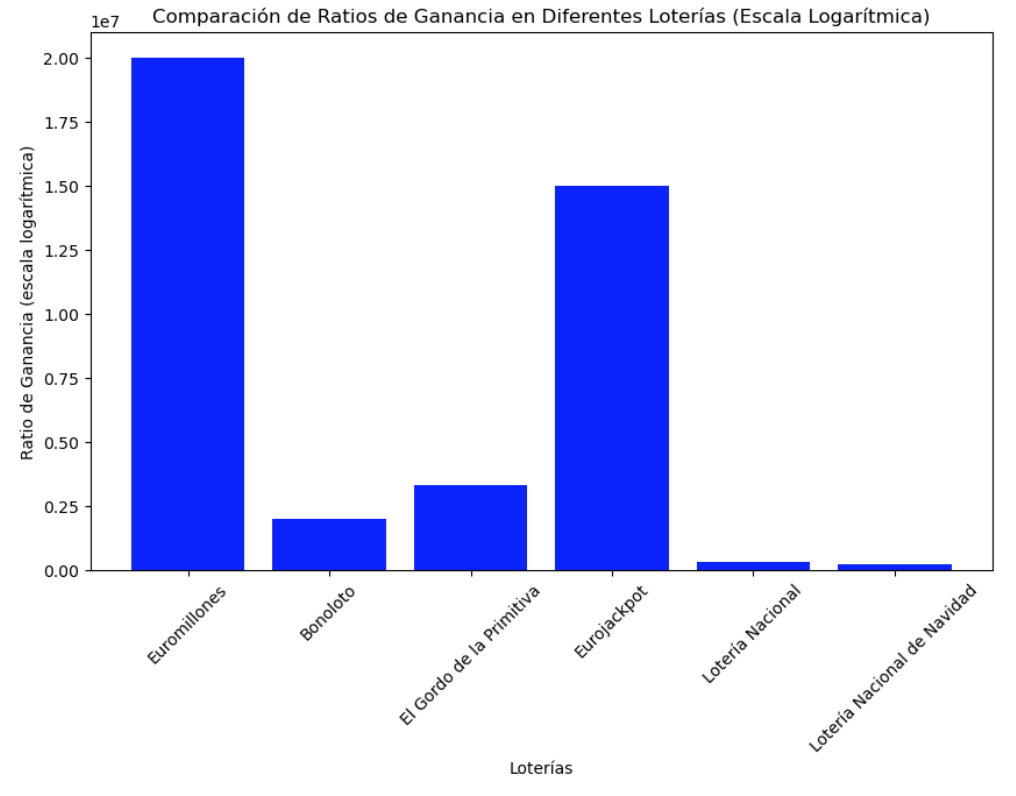
Como se puede apreciar en nuestro análisis, Euromillones destaca por tener el mayor ratio de ganancia entre las loterías estudiadas. Este alto ratio está directamente relacionado con la baja probabilidad de ganar en Euromillones. Aunque las posibilidades de acertar el premio mayor son extremadamente bajas, los premios ofrecidos son sustancialmente altos, lo que resulta en un ratio de ganancia elevado.
Es importante señalar que este análisis, aunque realizado de manera lúdica y en un momento de ocio, se basa en principios matemáticos y estadísticos básicos. Las loterías, por su naturaleza, están diseñadas con un equilibrio entre la probabilidad de ganar y el tamaño del premio. En juegos como Euromillones, un premio excepcionalmente alto compensa las bajas probabilidades de ganar, lo que se refleja en un ratio de ganancia alto.
Cabe destacar que este tipo de análisis no es una innovación o descubrimiento nuevo; las probabilidades y los ratios de ganancia son conceptos bien establecidos en el diseño y la operación de juegos de lotería. Sin embargo, el ejercicio de analizar estos datos es útil para entender mejor cómo funcionan estas loterías y qué pueden esperar los jugadores al participar en ellas.
Para presentar de manera efectiva la relación entre la probabilidad de ganar y el ratio de ganancia en las distintas loterías, se puede crear un gráfico que combine ambos aspectos. Este gráfico ayudará a visualizar cómo se correlacionan la probabilidad de ganar y el retorno potencial de la inversión en cada juego de lotería.
- Ejes del Gráfico:
– El eje horizontal (eje X) representa la probabilidad de ganar en cada lotería. .
– El eje vertical (eje Y) representa el ratio de ganancia de cada lotería.
- Puntos :
– Cada lotería se representaría con un punto . La posición de cada punto indicaría tanto la probabilidad de ganar (a lo largo del eje X) como el ratio de ganancia (a lo largo del eje Y).
- Interpretación:
– Un punto más hacia la derecha indicaría una menor probabilidad de ganar.
– Un punto más alto indicaría un mayor ratio de ganancia-inversión.
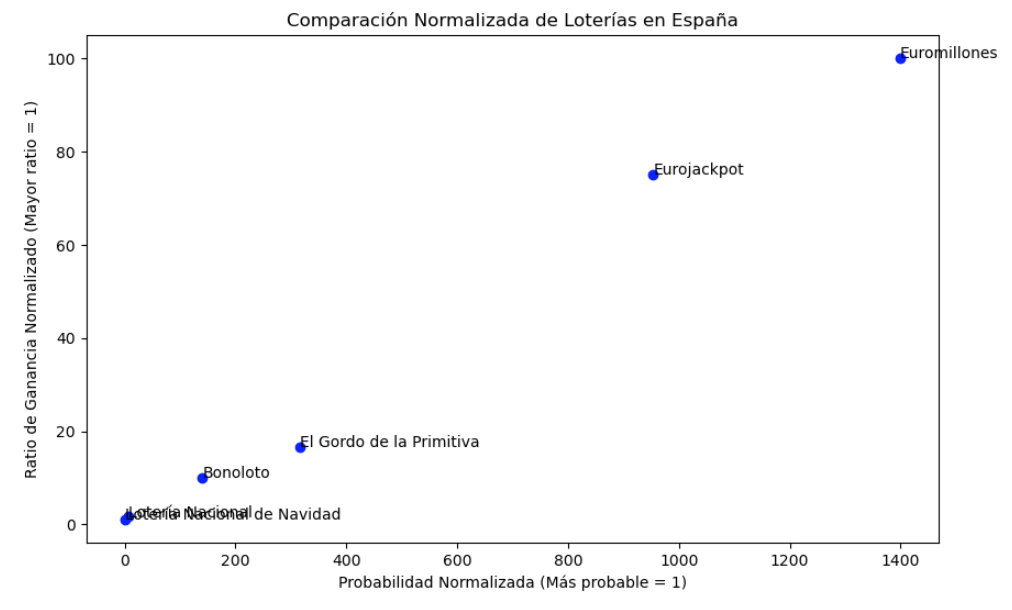
Al observar el gráfico que muestra la relación entre la probabilidad de ganar y el ratio de ganancia en las distintas loterías, se puede notar una clara relación lineal entre todas ellas. Este patrón lineal es indicativo de que los cálculos y el diseño de estas loterías siguen un modelo establecido, lo cual es lógico considerando que las loterías son, en última instancia, un modelo de negocio.
Esta relación lineal refleja cómo las organizaciones que gestionan las loterías equilibran las probabilidades de ganar con los premios ofrecidos para asegurar la viabilidad y sostenibilidad del juego. Por un lado, deben ofrecer premios lo suficientemente atractivos para motivar a las personas a comprar boletos. Por otro lado, necesitan asegurarse de que el modelo sea financieramente sostenible para poder continuar operando y generando ganancias.
El hecho de que exista una relación lineal entre la probabilidad de ganar y el ratio de ganancia sugiere que hay una fórmula o un enfoque coherente en la configuración de estos juegos. Esto implica que, aunque los premios grandes son menos probables, el potencial de ganancia se ajusta proporcionalmente para atraer a los jugadores.
Además, este equilibrio no solo se trata de las recompensas monetarias. Las loterías también ofrecen un valor intangible: la ilusión o la esperanza de ganar. Para muchos jugadores, el valor de soñar con un gran premio es una parte significativa de la experiencia de jugar a la lotería.
INTERPRETACIONES COMPARATIVAS
Para comprender mejor lo que realmente significa ganar la lotería, vamos a presentar diferentes comparaciones. Comencemos con una situación hipotética: ¿Qué tendría que suceder para garantizar que te toque la lotería? Imaginemos que juegas a la lotería una vez a la semana, incluyendo el sorteo especial de Navidad. Vamos a calcular cuántos años tendrías que seguir jugando a un juego específico de lotería para que, estadísticamente, te toque el premio mayor.
Para este cálculo, tomaremos la probabilidad de ganar el premio mayor en una lotería específica y la utilizaremos para estimar cuánto tiempo tendrías que jugar para que tus posibilidades de ganar se acerquen al 100%. Por ejemplo, si la probabilidad de ganar el Euromillones es de 1 en 139,838,160, ¿cuántos años tendrías que jugar semanalmente para que te toque?
Es importante tener en cuenta que este cálculo es puramente teórico y asume que cada sorteo es un evento independiente, lo que significa que jugar más veces no aumenta necesariamente tus probabilidades de ganar en un sorteo específico. Además, este enfoque no considera variables como cambios en las reglas del juego, la posibilidad de que otras personas ganen el premio, o incluso cambios en la cantidad de números a elegir.
Este tipo de análisis nos ayuda a poner en perspectiva lo que realmente significa “ganar la lotería” y a entender mejor la naturaleza de las probabilidades en juegos de azar.
Lotería Nacional de Navidad: 1.923 años
Lotería Nacional: 11.538 años
Bonoloto: 268.919 años
El Gordo de la Primitiva: 608.175 años
Euromillones: 2.689.195 años
La Primitiva: 268.919 años
Eurojackpot: 1.833.542 años
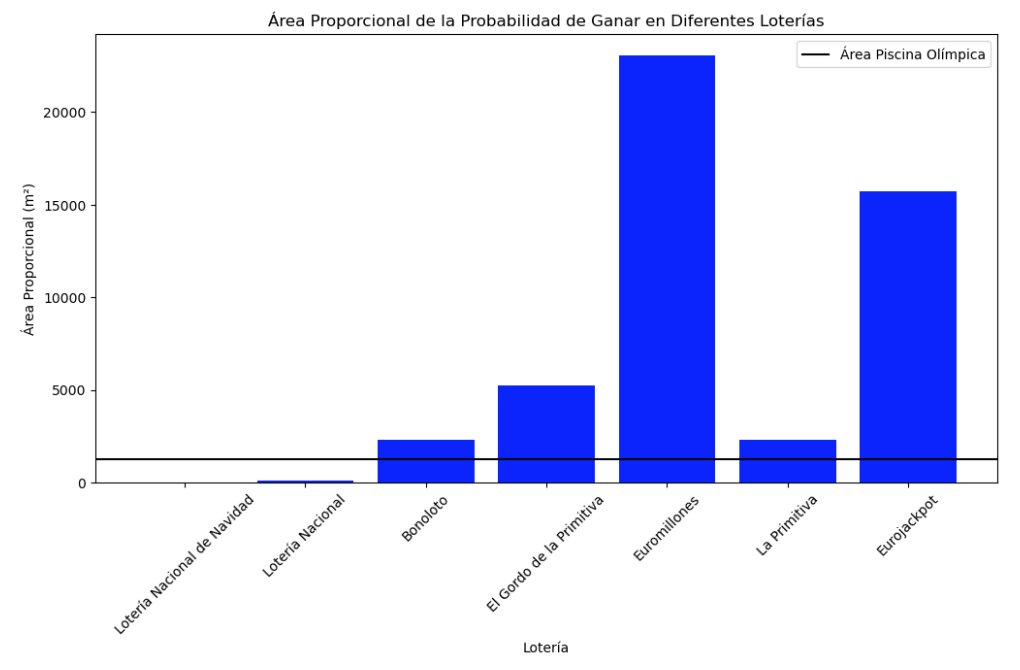
Para ilustrar las probabilidades de ganar en diferentes juegos de lotería, utilizaremos la analogía de una piscina olímpica llena de latas de refresco. Imagina que todas las latas son blancas, excepto una que es roja. La tarea es elegir, a ciegas, la lata roja para ganar. Esta analogía nos ayudará a visualizar cuán grande sería la piscina en cada juego de lotería, basándonos en sus respectivas probabilidades de ganar.
Lotería Nacional de Navidad: 0.01 piscinas olímpicas
Lotería Nacional: 0.08 piscinas olímpicas
Bonoloto: 1.85 piscinas olímpicas
El Gordo de la Primitiva: 4.17 piscinas olímpicas
Euromillones: 18.46 piscinas olímpicas
La Primitiva: 1.85 piscinas olímpicas
Eurojackpot: 12.59 piscinas olímpicas
Para visualizar aún más claramente las probabilidades de ganar en diferentes juegos de lotería, imaginemos una serie de imágenes que muestren el tamaño relativo de cada “piscina” necesaria para representar las probabilidades de cada juego (como de grandes son als piscinas entre ellas, de donde deberíamos elegir la lata). Usaremos la vista áerea de una piscina olímpica como referencia y adaptaremos el tamaño de cada piscina según las probabilidades de ganar en cada lotería.
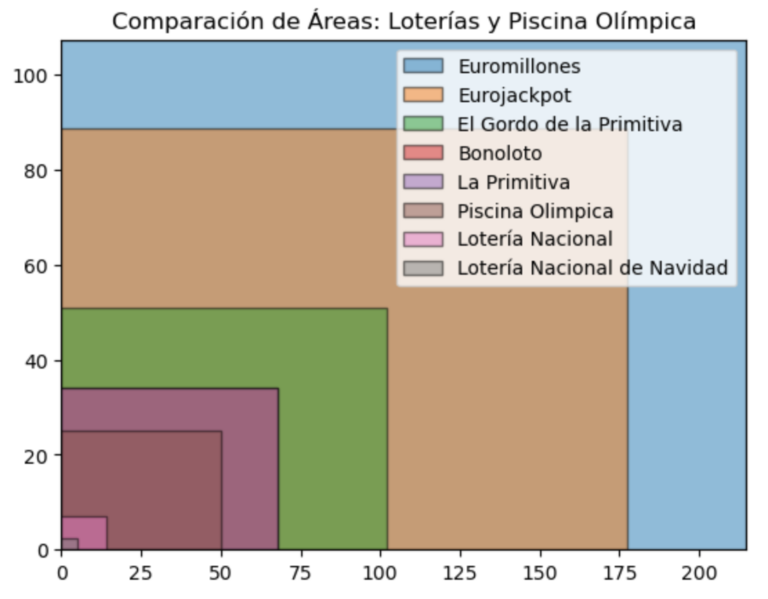
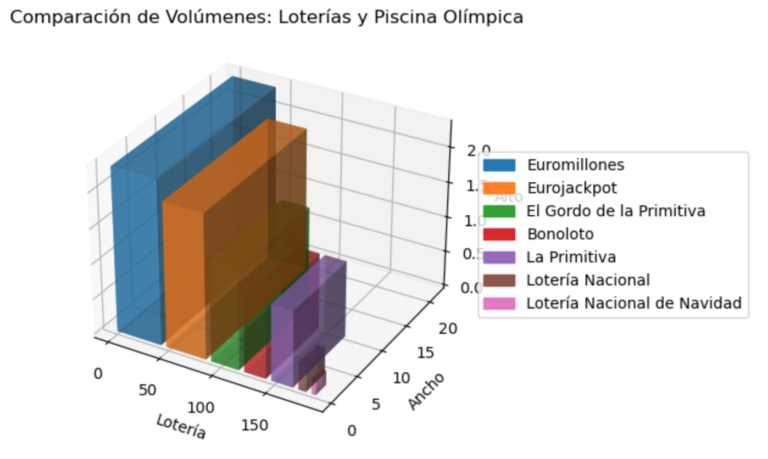
¡Y aquí va una pequeña confesión cómica sobre nuestro análisis! Todos los cálculos que hemos hecho, especialmente aquellos que involucran nuestra imaginativa piscina olímpica llena de latas de refresco, han sido realizados suponiendo que las latas son cúbicas. Sí, has leído bien: ¡latas cúbicas! Porque, seamos sinceros, si hubiéramos usado latas cilíndricas, tendríamos que haber considerado esos traviesos espacios vacíos entre ellas, ¡y eso es matemática avanzada que ni Pitágoras querría resolver en un día de piscina! Así que, por el bien de la simplicidad (y nuestra cordura), nuestras latas son tan cuadradas como los bloques de Minecraft. ¡Salud por las latas cúbicas y las probabilidades de lotería que nos hacen soñar! 🍹🎲🤣. Chiste al final del articulo.
Para proporcionar otra referencia visual que ayude a comprender las probabilidades de ganar en las loterías, utilizaremos la analogía de dos cubos: uno amarillo y uno rojo. Esta representación gráfica tiene como objetivo ilustrar de manera sencilla la diferencia entre la probabilidad total del juego y la probabilidad real que tiene un usuario individual de ganar.
- Cubo Amarillo – Probabilidad Total: El cubo amarillo representa el universo completo de posibilidades en un juego de lotería. Este cubo simboliza todas las combinaciones posibles de números o resultados que podrían ser elegidos en un sorteo. El tamaño del cubo amarillo varía según la lotería, siendo más grande en juegos con más combinaciones posibles (como Euromillones) y más pequeño en juegos con menos combinaciones (como la Lotería Nacional de Navidad).
- Cubo Rojo – Probabilidad Real del Usuario: Dentro del cubo amarillo, habrá un cubo rojo mucho más pequeño. Este cubo rojo representa la probabilidad real que tiene un usuario de ganar el premio mayor. En la mayoría de los juegos de lotería, este cubo rojo será extremadamente pequeño en comparación con el cubo amarillo, lo que ilustra visualmente cuán pequeñas son las probabilidades de ganar.
Al presentar estos cubos, los lectores podrán visualizar la diferencia entre el total de posibilidades en un juego de lotería y la probabilidad real de un jugador individual de ganar. Por ejemplo, en un juego con probabilidades de 1 en 100,000, el cubo rojo sería una fracción minúscula del tamaño del cubo amarillo. Esta representación ayuda a entender de manera intuitiva y gráfica la escala de las probabilidades en los juegos de lotería, proporcionando una perspectiva más clara de lo que realmente significa “una oportunidad en un millón” o similares.
Probabilidad loteria nacional de navidad
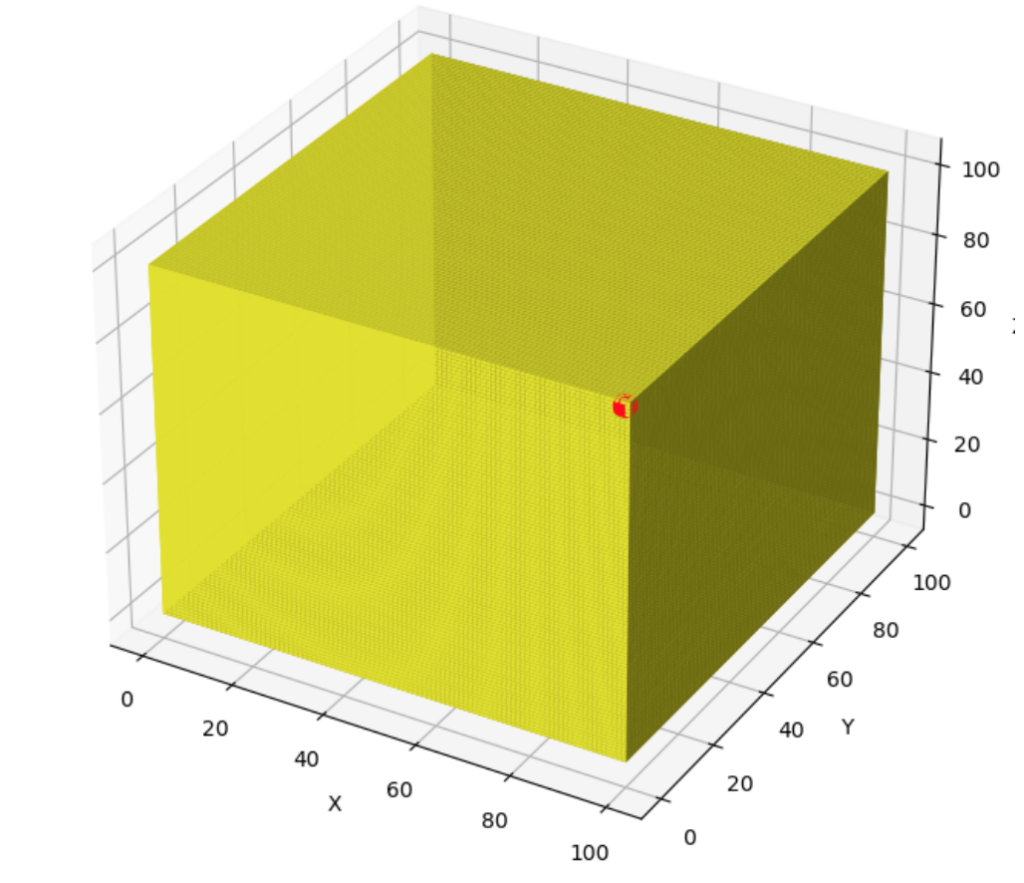
Probabilidad loteria nacional (semanal)

Probabilidad de las demas loterias
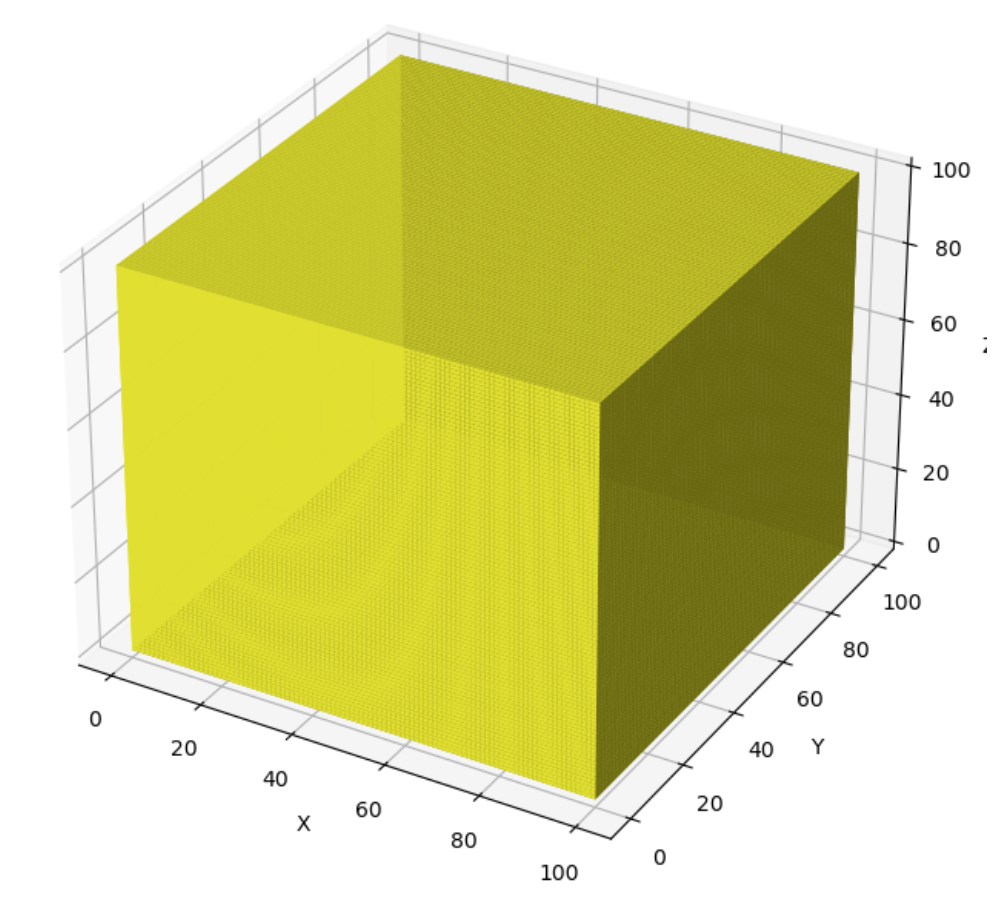
Efectivamente, en muchas loterías, la probabilidad real de ganar es tan pequeña que, en nuestra analogía visual de los cubos, el cubo rojo es imperceptible dentro del cubo amarillo.
CONCLUSIONES
En conclusión, todo lo expuesto en este análisis sobre las loterías ha sido un ejercicio teórico y de entretenimiento. Es importante recordar que, aunque hemos desglosado las probabilidades y realizado comparaciones creativas, nuestro objetivo nunca ha sido desalentar a nadie de participar en estos juegos. De hecho, la lotería, especialmente el Sorteo de Navidad en España, va mucho más allá de simples números y probabilidades.
El Sorteo de Navidad no es solo una tradición que aporta ilusión; es un tejido que conecta nuestra sociedad, convirtiéndose en una parte integral de nuestra cultura, especialmente durante las festividades navideñas. Compartir un décimo de lotería se ha convertido en un acto de unión, donde las personas reflexionan sobre con quién desearían compartir esa potencial fortuna. Esta práctica trasciende lo racional, destacando la cercanía y conexión con amigos y familiares.
Personalmente, siempre he percibido el Sorteo Especial de Navidad no tanto como una búsqueda de riqueza, sino como un reflejo del deseo humano de compartir suerte y fortuna con seres queridos. Es un ejemplo hermoso de cómo, incluso en algo tan basado en el azar como la lotería, lo que realmente valoramos es la oportunidad de compartir nuestra buena fortuna con aquellos que nos importan. En este sentido, la lotería se convierte en mucho más que un juego de azar; es un vehículo para expresar esperanza, amor y conexión durante una época del año muy especial.
CHISTE
Estaban un matemático, un ingeniero y un físico, y les piden que calculen el volumen de una vaca:
–Matemático– Si creo un sistema de ecuaciones que laminen a la vaca en infinitos planos calculando su área y recorro todo el largo de la vaca, conseguiré calcular el volumen,
–Físico– Si sumerjo una vaca en un tanque de agua, el agua que desplaza hacia arriba, es el volumen de la vaca.
–Ingeniero– Suponiendo una vaca esférica….
Curiosidad historica de la loteria y Voltaire
El método de Voltaire para ganar la lotería –> se hizo inmensamente rico <–.
En la historia de las finanzas y la literatura, pocas figuras brillan tanto como François-Marie Arouet, más conocido como Voltaire. Este emblemático escritor francés no solo dejó un legado literario inigualable, sino que también amasó una fortuna gracias a su astucia y la de su compañero, Charles Marie de la Condamine. Su historia es un fascinante relato de cómo un fallo en el sistema de lotería del siglo XVIII fue explotado magistralmente.
A principios del siglo XVIII, Francia se encontraba en una situación económica precaria, exacerbada por las consecuencias de la guerra de la Cuádruple Alianza. En un intento por estabilizar las finanzas nacionales, en 1727, el gobierno francés, bajo la dirección del ministro de Finanzas Michel Robert Le Pelletier-Desforts, implementó una medida drástica: reducir las tasas de interés de los bonos del Estado. Esta decisión provocó una devaluación significativa de los bonos, afectando la confianza en la economía francesa.
Para remediar la caída en el valor de los bonos y revitalizar la economía, Le Pelletier-Desforts introdujo una lotería vinculada a los bonos. Los propietarios de bonos podían adquirir boletos de lotería, cuyo precio dependía del valor nominal del bono. El premio de la lotería era sustancial: el valor original del bono más un extra de 500.000 libras francesas, una suma que podía asegurar una vida de riqueza.
Charles Marie de la Condamine, un matemático y amigo de Voltaire, identificó rápidamente una falla en este sistema. Observó que, independientemente del valor del bono, cada boleto de lotería tenía la misma probabilidad de ganar. Esto significaba que comprar boletos de lotería para bonos de bajo valor era mucho más rentable. Voltaire y De la Condamine, junto con otros inversores, comenzaron a adquirir masivamente estos bonos devaluados y, por ende, boletos de lotería baratos, aumentando exponencialmente sus posibilidades de ganar.
Para no levantar sospechas, Voltaire llegó a un acuerdo con un notario para la compra de los boletos. Cada mes, compraban grandes cantidades de boletos, y regularmente ganaban el premio mayor. Sin embargo, la naturaleza rebelde de Voltaire eventualmente llevó a las autoridades a descubrir el esquema. A pesar de esto, un juicio determinó que no estaban haciendo nada ilegal. Como resultado, los miembros de este grupo se enriquecieron enormemente, y el gobierno se vio obligado a cerrar la lotería y a despedir a Le Pelletier-Desforts.
La historia de Voltaire y De la Condamine es un ejemplo fascinante de cómo la agudeza intelectual y un profundo conocimiento de las finanzas y las matemáticas pueden ser utilizados para explotar las debilidades de un sistema económico. Este episodio no solo aseguró la fortuna de Voltaire, permitiéndole dedicarse a la escritura, sino que también financió las expediciones científicas de De la Condamine, incluyendo importantes descubrimientos geográficos y científicos. En última instancia, este evento destaca cómo un error en un sistema financiero gubernamental llevó a consecuencias inesperadas y cambió el curso de varias vidas y, en cierta medida, de la historia misma.

